
Math has unique characteristics that do not present themselves in other subjects. If you do not understand these characteristics, it may cause a problem later on.
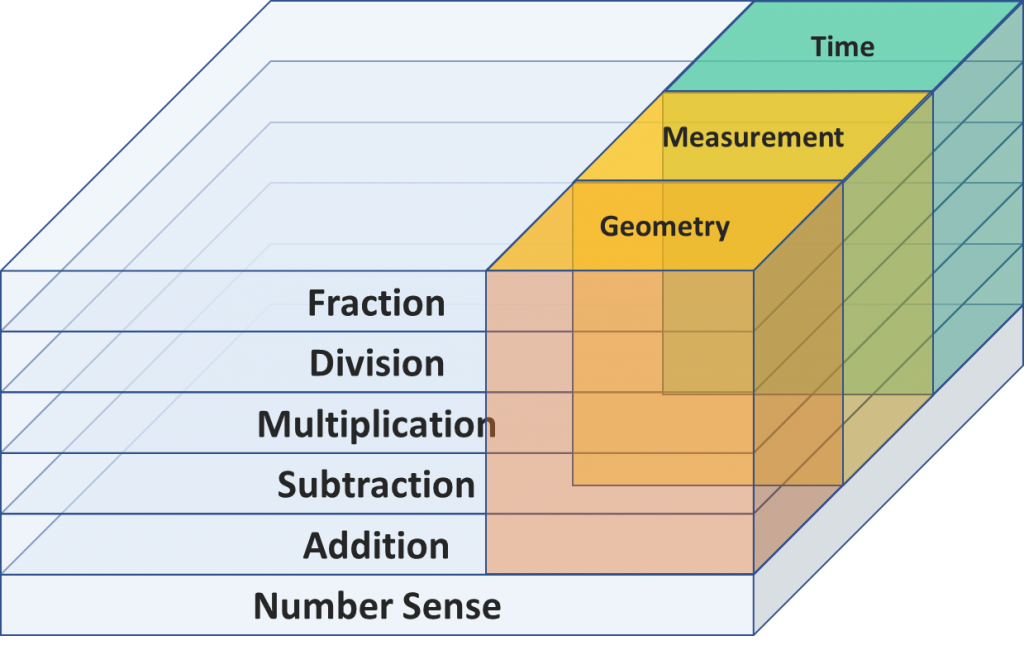
Math builds upon itself and requires a solid understanding of previous skills in order to grasp new concepts. For example:
Therefore, if your child does not have a solid understanding of number sense, your child’s knowledge of any concept going forward will never be stronger than your child’s number sense abilities. If your child does not know addition well, your child will not fare well in all concepts to come that utilize addition.
On the other hand, grasping concepts in subjects such as language arts or social studies has little to no dependency on one’s understanding of concepts previously covered.
In other words, math is a vertical subject, while others are horizontal with little to no vertical dependency.
Structure of Math Concepts
You may not be too concerned if your child scores 70 points on a single test in language arts or social studies, but in math, scoring 70 points on even one exam is a matter that should be promptly addressed. As discussed above, math is a vertical subject. A score of 70 points nearly guarantees that your child will have a tough time keeping up in math, especially in grades four through six.
Conceptually: 70% (number sense) x 70% (addition) x 70% (subtraction) x 70% (multiplication) x 70% (division) x 70% (fractions) = 11.8%
How can your child understand future concepts such as “Ratios” that will build on top of his or her current knowledge if your child’s current understanding is no better than 11.8%? Now you understand why students start giving up math while learning fraction and ratios.
You might think this is too simplified, but having observed many students struggle with math – especially fractions and ratios – the majority do not have a solid understanding of arithmetic. The calculation above aligns with what we’ve observed in our experience.
Another unusual characteristic of math is that it requires strong proficiency and that proficiency in one area will directly affect proficiency in subsequent skills to be learned. I see a significant discrepancy in the amount of emphasis on proficiency between Asian families and families of other races. Asian families typically emphasize proficiency in arithmetic. The reality is that proficiency in basic arithmetic – especially addition, subtraction, and multiplication – is crucial to building one’s mathematical skillset. Knowing how to calculate is not enough. It takes time to calculate, and time isn’t always a given in the real world. Many parents do not push their children enough in proficiency, and it’s a huge mistake.
Unfortunately, taking too long to solve an arithmetic problem is akin to not being able to solve the problem at all, as all tests impose a time limit. You need to recognize that understanding a concept and being able to apply that concept are separate endeavors. For example, many students understand carryover addition, subtraction with regrouping, and multiplication, but take too long to calculate solutions to such problems. These students cannot solve problems in time.
Furthermore, a lack of proficiency hinders students from grasping new concepts. In the process of mastering multiplication, students often use addition in place of multiplication if they haven’t fully memorized the multiplication table.
For example, to calculate 8 x 7, many students calculate 8 x 5 + 8 + 8 if they cannot recall 8 x 7 from memory. This lack of proficiency hinders their ability to master multiplication.
Children need to remember two-number combinations that sum up to 10, 45 carryover patterns, and the multiplication table – and they need to be able to instantly solve all of the above. Memorizing these patterns is simple and does not require much effort – usually, two or so weeks for the 45 carryover patterns and another two to three weeks for the multiplication table will suffice. Becoming proficient in these calculations brings about an unbelievable difference in both skill and confidence.
If your child seems to understand how to calculate addition with carryover and subtraction with regrouping, but still struggling to get a good score, check the proficiency. Lack of proficiency hinders to learn new concepts such as multiplication, division, fraction. So, make sure that your child does not only understand the key concepts such as carryover and regrouping but also the proficiency enough on these.
Many students who understand concepts but do not score well in math are lacking in proficiency. Proficiency also directly affects a child’s confidence in his or her math skills.
If your child seems to understand addition with carryover and subtraction with regrouping but still struggles to score well in math, evaluate your child’s proficiency. Make sure that your child both understands key concepts and is proficient in those concepts.
Another challenge in math is that it is difficult to determine whether your child understands a concept or a technique. Your child can remember combinations of addition and multiplication, carryover, and regrouping. They can remember tables and techniques without understanding the underlying concepts. With technique alone, they can score 100 on a test without understanding concepts. Depending too much on techniques could be a downside of highly emphasizing proficiency.
These students are great students who follow parental instructions, practice often, score well, and master techniques. However, these students start to struggle late in elementary school, around fourth grade or so. It’s unfortunate, but not uncommon.
Students who do not fully grasp number sense start to struggle when dealing with decimals and large numbers.
Students who do not understand the number sense fully, start struggling in decimal and large numbers.
Students who master multiplication and division technically, but not conceptually, are faced with similar circumstances – they struggle with word problems and do not know how to apply their skills.
Children who did not play with tangible objects to practice counting tend to struggle with number sense, but this varies widely from individual to individual. Some children grasp concepts instantly, and some need a much longer time.
Fractions and ratios are no exception. Students need to grasp concepts in order to apply them correctly to world problems. Please make sure your child fully understands a concept, teach related techniques, and have your child practice for proficiency.
1. Math test scores should always be close to 100%, as math is a vertically integrated subject.
2. Proficiency in arithmetic is crucial.
3. Ensure that your child fully understands concepts.
*A note based on research conducted by UC Irvine on the relative importance of adolescent skills and behaviors for adult earnings: In a cross-national study, math has demonstrated the highest correlation between the completion of school and earnings among major subjects. Ensure that your child is skilled in math.
